课程笔记：机器学习基础  Week 6

学习目标

1. 将SVD应用于特定数据集

2. 在特定背景下分析PCA的结果

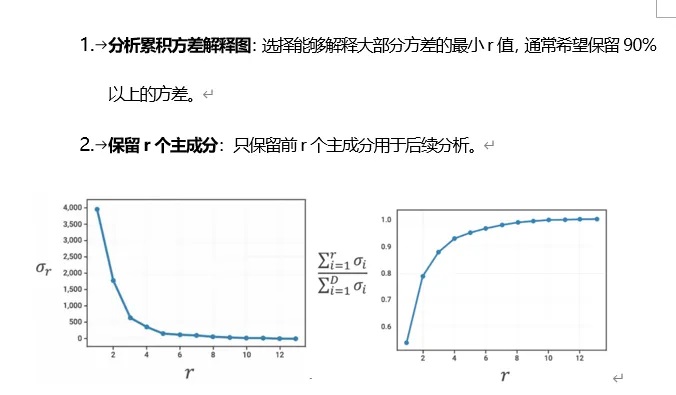
3. 绘制并解释奇异值（碎石图）

4. 选择r值以达到期望的方差捕获水平

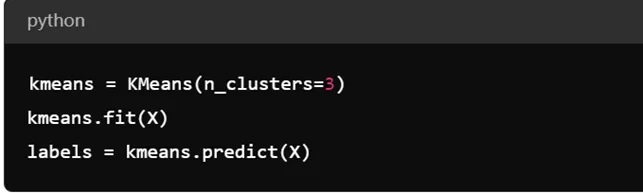
5. 在Python中实现K-Means算法

6. 在Python中应用K-Means函数

7. 在给定初始数据集的情况下解释K-Means和PCA的结果

8. 使用scikit-learn进行K-Means聚类

9. 比较两种不同的质心初始化方法（k-means++ vs. 随机初始化）

10. 比较在给定数据集上的多种聚类技术的结果

应用SVD到特定数据集

要点：

• 数据归一化：首先通过减去均值并除以标准差对数据进行归一化处理。

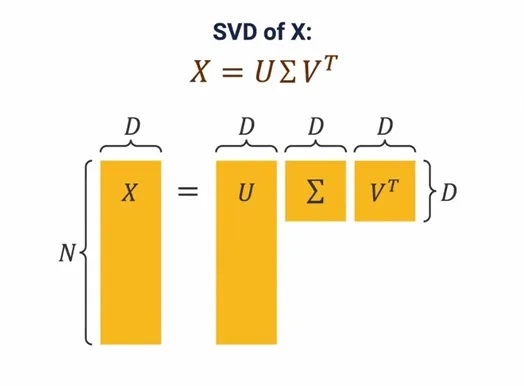
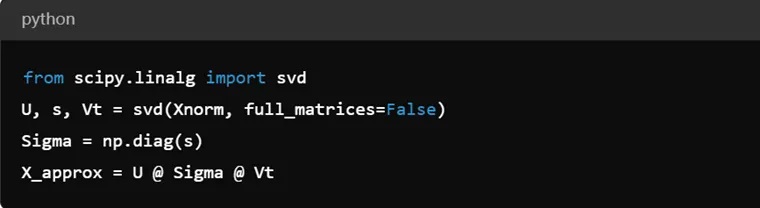
• 执行SVD：在归一化的数据上执行奇异值分解（SVD）。

• 验证分解：通过矩阵乘法重构原始数据，并检查结果是否与归一化数据一致

  思路：
  

• SVD将数据矩阵分解为三个矩阵 U、Σ和V^T，其中 U和 V分别是左奇异矩阵和右奇异矩阵，Σ是对角矩阵，包含奇异值。

• 数据归一化确保各特征的标准差为1，并将数据的均值移到0，这对于后续的SVD计算至关重要。

2. 分析PCA的结果

步骤：

 

关键点：

3. 绘制和解释奇异值（碎石图）

步骤：

思路：

4. 选择r值以达到所需的方差捕获水平

步骤：

5. 在Python中实现K-Means算法

步骤：

思路：

6. 在Python中应用K-Means函数

步骤：

7. 解释K-Means和PCA的结果

思路：

8. 使用Scikit-Learn进行K-Means聚类

步骤：

9. 比较初始化方法（k-means++ vs. 随机初始化）

关键点：

10. 比较多种聚类技术

技术：

比较：

Week 7

 

学习目标

1.区分线性模型和非线性模型

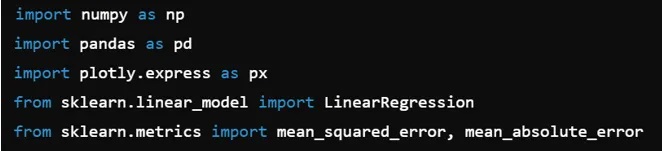
2.使用Plotly拟合简单线性回归线

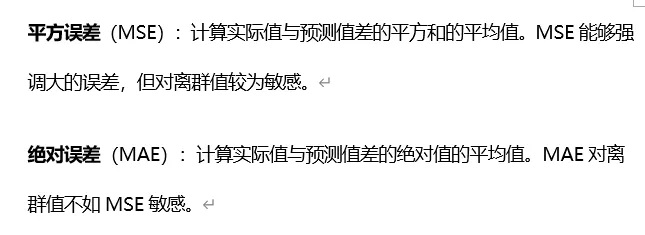
3.计算平方误差和绝对误差

4.识别损失函数对离群值的反应

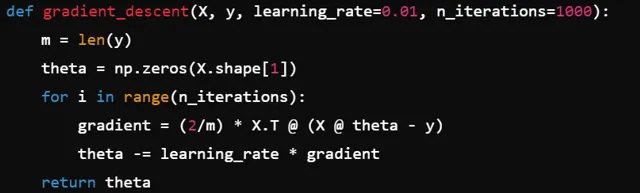
5.应用多种技术来最小化损失函数

6.使用多元线性回归模型预测结果

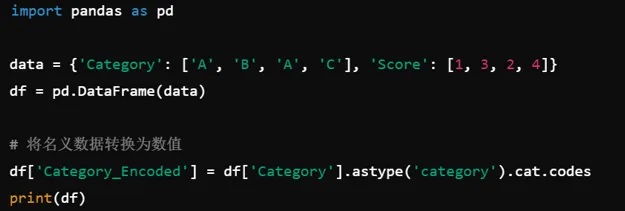
7.识别数据集中序数、名义和分类数据

2. 如何拟合线性回归

步骤：

代码： 

导入必要的数据库：

构建模型：

回归模型可视化：

3. 如何计算平方误差和绝对误差

代码：

4.如何识别损失函数对离群值的反应

5. 应用多种技术来最小化损失函数

代码：

代码：

7. 识别数据中的序数、名义和分类数据

代码：

Author

作者简介

01

作者：粟登洋

01

中国矿业大学(北京）人工智能硕士 实习工程师

研究方向为选矿设备、选矿流程的智能化。本科期间曾获全国大学生数学竞赛二等奖、北京市大学生数学竞赛一等奖、矿大（北京）第九届力学竞赛二等奖、校奖学金等。研究生阶段。

02

研究生导师：徐宏祥

03

中国矿业大学（北京） 副教授 博导

博士毕业于中国矿业大学，矿物加工工程专业（导师：刘炯天院士）。美国哥伦比亚大学，环境工程系联合培养博士（导师：Ponisseril Somasundaran 教授）。目前在中国矿业大学（北京）担任化环学院矿加系主任，博士生导师。曾主持多项国家/省级科研课题。主要研究方向包括：微细粒分选理论及选矿工艺、低品质煤高效分选过程强化、工业水处理、分子动力学模拟、矿物资源综合利用、矿物加工设备智能化等。

了解更多

联系方式

陈经理

微信：C1184531314

    网址：

   www.alpha1888.com （中文站）

   www.alpha-technology.com.au(英文站）

END